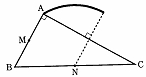垽昋導岞棫崅峑擖帋栤戣丒嶰暯曽偺掕棟栤戣廤
佢俙亖90亱丆佢俛亖60亱丆俙俛亖6 cm偺捈妏嶰妏宍俙俛俠偑偁傝丆曈俙俛丆俛俠偺拞揰傪偦傟偧傟揰俵丆俶偲偡傞丅塃偺恾侾偺傛偆偵丆慄暘俵俙忋偵揰俹傪偲傝丆曈俙俠忋偵揰俻傪佢俹俶俻亖90亱偲側傞傛偆偵偲傞丅
偙偺偲偒丆師偺栤偄偵摎偊側偝偄丅乮墌廃棪偼兾傪梡偄傞偙偲丅乯
侾丂揰俹偑揰俵偺埵抲偵偁傞偲偒丆慄暘俙俻偺挿偝傪媮傔傛丅
俀丂塃偺恾俀偺傛偆偵丆捈慄PN偵偮偄偰揰俛偲斀懳懁偵丆佢PNB亖佢PND丆NB亖NC亖ND偲側傞揰D傪偲傞丅
(1)丂仮俠俶俻佭仮俢俶俻偱偁傞偙偲傪徹柧偣傛丅
(2)丂佢俛俶俹亖43亱偺偲偒丆仮俢俹俻偵偍偗傞佢俢俹俻偺戝偒偝偼壗搙偐丅
(3)丂揰P偑慄暘MA忋傪揰M偐傜揰A傑偱摦偔偲偒丆揰D偑摦偄偰偱偒傞慄傪夝摎梡巻偺恾偵偐偒擖傟傛丅傑偨丆偦偺慄偺挿偝傪媮傔傛丅
恾侾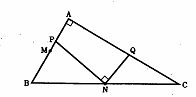
恾俀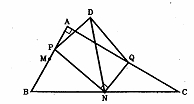
夝偗傑偟偨偐丠偦傟偱偼夝摎偱偡丅
侾丂仩AMNQ偼挿曽宍偲側傞丅拞揰捈寢掕棟傛傝3併3乮cm乯
俀丂(1) 乮徹柧乯仮CNQ偲仮DNQ偵偍偄偰
嫟捠側曈偩偐傜丂NQ亖NQ乧乧嘆
壖掕傛傝丂丂丂丂NC亖ND乧乧嘇
傑偨丆佢CNQ亖90亱亅佢PNB丆佢DNQ亖90亱亅佢PND丆偱
佢PNB亖佢PND丆偩偐傜丂佢CNQ亖佢DNQ乧乧嘊
嘆丆嘇丆嘊傛傝丆俀曈偲偦偺娫偺妏偑偦傟偧傟摍偟偄偺偱丂仮CNQ佭仮DNQ
(2)丂仮CNQ佭仮DNQ偵傛傝丂佢NCQ亖佢NDQ乧乧嘆
仮BNP佭仮DNP偵傛傝丂佢PBN亖佢PDN乧乧嘇
堦曽丆仮ABC偵偍偄偰丂佢PBN亄佢NCQ亖90亱丆偩偐傜
嘆丆嘇傛傝丂佢PDN亄佢NDQ亖90亱丆偮傑傝丂佢PDQ亖90亱
傛偭偰丆仩PDQN偵偍偄偰丂佢PDQ亄佢PNQ亖180亱
偟偨偑偭偰係揰P丆D丆Q丆N偼摨堦墌廃忋偵偁傞丅
備偊偵佨DQ偺墌廃妏傛傝丂佢DPQ亖佢DNQ亖(180亱亅2佢BNP)亖90亱亅佢BNP亖47乮搙乯
(3)丂揰D偼丆揰N傪拞怱偵丆敿宎NA偺墌廃忋傪揰A偐傜丆拞怱妏60亱偺愵宍傪偊偑偔丅
傛偭偰丂60亐360亊(2亊6亊兾)亖2兾 (cm)
壓偺恾